Sayı

Sayı, sayma, ölçme ve etiketleme için kullanılan bir matematiksel nesnedir. En temel örnek, doğal sayılardır (1, 2, 3, 4 ve devamı). Sayılar, (numeral) ile dilde temsil edilebilir. Daha evrensel olarak, tekil sayılar rakam adı verilen sembollerle temsil edilebilir; örneğin, "5" beş sayısını temsil eden bir rakamdır. Yalnızca nispeten az sayıda sembolün ezberlenebilmesi nedeniyle, temel rakamlar genellikle bir rakam sisteminde organize edilir, bu da herhangi bir sayıyı temsil etmenin organize bir yoludur. En yaygın rakam sistemi Hint-Arap rakam sistemidir, bu sistem on temel sayısal sembol, yani rakam kullanılarak herhangi bir negatif olmayan tam sayının temsil edilmesine olanak tanır. Sayılar sayma ve ölçme dışında, etiketlerde (telefon numaraları gibi), sıralamada (seri numaraları gibi) ve kodlarda (ISBN'ler gibi) kullanılmak için de sıklıkla kullanılır. Yaygın kullanımda, bir rakam ile temsil ettiği sayı net bir şekilde ayrılmaz.

Matematikte, sayı kavramı yüzyıllar boyunca peyderpey genişletilmiştir: sıfır (0),negatif sayılar,${\displaystyle \left({\tfrac {1}{2}}\right)}$ gibi rasyonel sayılar, karekök 2 ${\displaystyle \left({\sqrt {2}}\right)}$ ve π gibi gerçek sayılar, ve gerçek sayıları −1'in karekökü ile genişleten karmaşık sayılar buna dahil edilmiştir. Sayılarla yapılan aritmetik işlemler ile yapılır; en bilindik işlemler toplama, çıkarma, çarpma, bölme ve üs almadır. Bunların çalışılması veya kullanılması aritmetik olarak adlandırılır, bu terim ayrıca sayıların özelliklerinin incelendiği sayılar teorisini de ifade edebilir.

Sayıların pratik kullanımlarının yanı sıra, dünya genelinde kültürel bir önemi de bulunmaktadır. Örneğin, Batı toplumunda, 13 sayısı genellikle uğursuz olarak kabul edilir ve "milyon", kesin bir miktar yerine "çok" anlamına gelebilir. Artık sahte bilim olarak kabul edilse de, sayıların mistik bir önemine dair inanç, bilinen adıyla nümeroloji, antik ve Orta Çağ düşüncelerine derinden işlemiştir. Nümeroloji, Yunan matematiğinin gelişimini büyük ölçüde etkilemiş ve günümüzde hala ilgi çeken birçok sayı teorisi problemi üzerine araştırmaları teşvik etmiştir.

19. yüzyılda matematikçiler, sayıların bazı özelliklerini paylaşan ve kavramı genişletiyor olarak görülebilecek pek çok farklı soyutlama geliştirmeye başladılar. İlkler arasında, karmaşık sayı sistemini çeşitli şekillerde genişleten veya değiştiren bulunmaktadır. Modern matematikte, sayı sistemleri, halkalar ve alanlar gibi daha genel cebirsel yapıların önemli özel örnekleri olarak kabul edilir ve "sayı" teriminin uygulanması, temel bir öneme sahip olmaksızın, bir konvansiyon meselesidir.

Tarihçe

Sayıların ilk kullanımı

Kemikler ve üzerlerine kesik izleri yapılmış diğer eserler ile keşfedilmiştir ki, birçok kişi bunların olduğuna inanmaktadır. Bu çeteleler, geçen zamanın, örneğin gün sayısının, ay döngülerinin sayılması ya da çeşitli miktarların, örneğin hayvan sayılarının kaydı, tutulması için kullanılmış olabilir.

Bu çetele - çizik atma sistemi, modern ondalık gösterimdeki gibi basamak değeri kavramına sahip değildir. Bu da büyük sayıların temsilini sınırlar. Yine de, çetele - çizik atma sistemleri, ilk tür soyut sayı sistemi olarak kabul edilir.

Basamak kavramına sahip bilinen ilk sistem, M.Ö. 3400 civarına ait Antik Mezopotamya ölçü birimleri sistemidir ve bilinen en eski onlu sayı sistemi ise M.Ö. 3100 yılında Mısır'da gözlemlenmiştir.

Rakamlar

Sayılar, sayıları temsil etmek için kullanılan semboller olan rakamlardan ayırt edilmelidir. Mısırlılar ilk şifreli rakam sistemini icat ettiler ve Yunanlılar sayma sayılarını İyon ve Dorik alfabesine aktararak bu yöntemi takip ettiler. Roma rakamları, Roma alfabesinden harflerin kombinasyonlarını kullanan bir sistem, Avrupa'da 14. yüzyılın sonlarına doğru Hint-Arap rakam sisteminin yayılmasına kadar baskın kaldı ve Hint-Arap rakam sistemi günümüzde dünyada sayıları temsil etmek için kullanılan en yaygın sistem oldu. Bu sistemin etkinliğinin sebebinin, M.S. 500 civarında antik Hintli matematikçiler tarafından geliştirilen sıfır sembolü olduğu düşünülmektedir.

Sıfır

M.S. 683 tarihli bir yazıttan alınan ile yazılmış '605' sayısı. Sıfırın ondalık bir rakam olarak erken bir kullanımıdır.

Sıfır'ın belgelenmiş ilk bilinen kullanımı M.S. 628 yılına aittir ve içinde, Hintli matematikçi Brahmagupta'nın ana eserinde yer alır. Brahmagupta, 0'ı bir sayı olarak ele almış ve aralarında de dahil olmak üzere, sıfırı içeren işlemleri tartışmıştır. Bu dönemde (7. yüzyıl), sıfır kavramı Kamboçya'ya olarak ulaşırken sıfırın daha sonra Çin ve İslam dünyasına yayıldığı görülmektedir.

Brāhmasphuṭasiddhānta adlı eseriyle Brahmagupta, sıfırı sayı olarak ele alan bilinen ilk metni yazmıştır ve bu yüzden sıklıkla sıfır konseptini ilk tanımlayan kişi olarak görülür. Brahmagupta, sıfırın hem negatif hem de pozitif sayılarla birlikte kullanılabilmesine yönelik kurallar belirlemiştir; mesela "pozitif bir sayıya sıfır eklenirse sonuç yine pozitif sayı olur, negatif bir sayıya sıfır eklenirse sonuç negatif sayı olur" gibi. Brāhmasphuṭasiddhānta, sıfırı yalnızca diğer bir sayının yerini tutan bir sembol ya da miktarın olmamasını belirten bir işaret olarak değil, aynı zamanda bağımsız bir sayı olarak kabul eden ilk yazılı kaynaklardan biridir ve bu özelliğiyle Babil matematiğinden ya da Ptolemy ve Romalıların yaklaşımlarından ayrılır.

0 sayısının kullanımı, basamak sistemlerinde bir yer tutucu rakam olarak kullanımından ayrılmalıdır. Birçok antik metin 0 rakamını kullanmıştır. Babil ve Mısır metinlerinde bu kullanıma rastlanır. Mısırlılar, çift girişli muhasebe sistemlerinde sıfır bakiyeyi belirtmek için nfr kelimesini kullanmışlardır. Hint metinleri, boşluk kavramını ifade etmek için Sanskritçe Shunye veya shunya kelimesini kullanmıştır. Matematik metinlerinde bu kelime genellikle sıfır sayısına atıfta bulunur. Benzer şekilde, M.Ö. 5. yüzyılda Panini Sanskrit dilinin cebirsel bir dilbilgisi için erken bir örnek olan 'de boş (sıfır) işlevsel sözcüğünü kullanmıştır (ayrıca 'ya bakınız).

Meksika'nın güney-orta bölgesinde yaşayan geç dönem Olmek halkı, Yeni Dünya'da, muhtemelen M.Ö. 4. yüzyılda ama kesinlikle M.Ö. 40 yılına kadar, sıfır için bir sembol, bir kabuk glifi kullanmaya başlamıştır. Bu sembol, Maya rakamlarının ve Maya takviminin ayrılmaz bir parçası haline gelir. Maya matematiği, temel olarak 4 ve 5'i, 20 tabanında yazılmış olarak kullanmıştır. George I. Sánchez, 1961'de temel 4, temel 5 "parmak" abaküsünü yayımlar.

M.S. 130 yılına gelindiğinde, Hipparkos ve Babillilerden etkilenen Ptolemy, altmışlık sayı sistemi içinde başka bir yerde Yunan rakamları kullanırken 0 için uzun bir üst çizgi ile küçük bir daire şeklinde bir sembol kullanıyordu. Yalnızca bir yer tutucu olarak değil, tek başına kullanıldığı için bu (Helenistik sıfır), Eski Dünya'da belgelenmiş gerçek bir sıfırın ilk kullanımıydı. Daha sonraki Bizans elyazmalarında, Syntaxis Mathematica (Almagest) eserinde, Helenistik sıfır Yunan harfi Omikron'a (aksi takdirde anlamı 70) dönüşmüştü.

Bir başka özgün sıfır simgesi, 525 yılında Dionysius Exiguus tarafından ilk kez belgelendirilmiş olup, Roma rakamlarının yanı sıra tablolarda yer almıştır; ancak bu, bir sembol yerine "hiçlik" anlamına gelen "nulla" kelimesi şeklinde ifade edilmiştir. Bir bölme işlemi sonucunda kalan olarak 0 elde edildiğinde, yine "hiçlik" anlamına gelen "nihil" kelimesi tercih edilmiştir. Bu Orta Çağ dönemi sıfırları, sonraki dönemlerde Paskalya'nın hesaplanmasında görev alan tüm Orta Çağ hesapçıları tarafından kullanılmıştır. N harfinin tek başına kullanımı, Bede ya da bir çalışma arkadaşı tarafından yaklaşık 725 yılında Roma rakamlarının yer aldığı bir tabloda gerçek bir sıfır simgesi olarak kullanılmıştır.

Negatif sayılar

Negatif sayı kavramının soyut bir anlayışı, M.Ö. 100–50 yılları arasında Çin'de erkenden kabul görmüştür. Matematik Sanatı Üzerine Dokuz Bölüm adlı eser, geometrik şekillerin alanlarının hesaplanması yöntemlerini sunmakta ve bu bağlamda kırmızı çubuklar pozitif katsayıları, siyah çubuklar ise negatif katsayıları temsil etmek üzere kullanılmıştır. Batı literatüründe negatif sayılara dair ilk atıf, M.S. 3. yüzyılda Yunanistan'da kaydedilmiştir. Diophantus, Arithmetika eserinde 4x + 20 = 0 (çözüm negatif) denklemine değinmiş ve bu denklemin mantıksız bir sonuç ortaya koyduğunu ifade etmiştir.

600'lerde, Hindistan'da negatif sayılar, borç miktarlarını ifade etme amacıyla kullanılmaya başlanmıştır. Diophantus'un daha önceki bahsi, 628 yılında Brāhmasphuṭasiddhānta eseriyle Brahmagupta tarafından daha detaylı bir şekilde ele alınmıştır. Brahmagupta, günümüzde de kullanılan genel ikinci dereceden denklem formülünün üretimi için negatif sayıları kullanmıştır. Ancak, 12. yüzyılda Hindistan'da Bhaskara, ikinci dereceden denklemler için negatif kökler sunmuş, fakat negatif değerin "bu durumda dikkate alınmaması gerektiğini, çünkü yetersiz olduğunu; negatif köklerin kabul görmediğini" ifade etmiştir.

17. yüzyıla dek Avrupa'daki matematikçiler genellikle negatif sayılar konseptine karşı çıkmışlardır; ancak Fibonacci, bu sayıların borçlar olarak yorumlanabileceği finansal sorunlarda negatif çözümlere yer vermiştir (, 13. bölüm, 1202) ve sonraki çalışmalarında zararlar bağlamında da bunu sürdürmüştür (Flos'ta). René Descartes, cebirsel polinomlarda karşılaştığı negatif kökleri "yanlış kökler" olarak nitelendirmiş, fakat zamanla gerçek köklerle yanlış kökler arasında bir yer değiştirme yöntemi geliştirmiştir. Bu dönemde Çinliler, pozitif sayının karşılık gelen rakamının en sağdaki sıfır olmayan basamağının üzerine çapraz bir çizgi çekerek negatif sayıları göstermekteydi. Negatif sayıların bir Avrupa çalışmasında kullanımına ilk rastlanan örnek, 15. yüzyılda tarafından gerçekleştirilmiştir. Chuquet, bu sayıları üsler olarak kullanmış, ancak onlara "absürt sayılar" demiştir.

18. yüzyıla dek matematiksel pratiklerde, denklemlerden elde edilen negatif sonuçların anlamsız olduğu kabulüyle bu tür sonuçların dikkate alınmaması genel bir yaklaşımdı.

Rasyonel sayılar

Kesirli sayı kavramının tarihöncesi dönemlere uzandığı düşünülmektedir. Antik Mısır uygarlığı, Rhind Matematik Papirüsü ve gibi matematiksel dokümanlarında rasyonel sayılar için özel bir notasyonu geliştirmiştir. Antik Yunan ve Hint matematikçiler, sayı teorisinin genel incelemesi çerçevesinde, rasyonel sayılar teorisine dair çalışmalar yapmışlardır. Bu çalışmalar arasında en meşhuru, M.Ö. 300 yıllarına tarihlenen Öklid'in Elementleri eseridir. Hint literatüründe ise, matematiksel çalışmaların genel bir parçası olarak sayı teorisini ele alan ön plana çıkmaktadır.

Ondalık kesirlerin kavramı, ondalık basamak gösterimiyle sıkı bir bağlantıya sahiptir ve bu iki kavramın paralel olarak geliştiği düşünülmektedir. Örneğin, Jain matematiğine ait sutralarda pi sayısının veya 2'nin kare kökünün ondalık kesir yaklaşıklarının hesaplamaları sıkça yer almaktadır. Ayrıca, Babil matematik metinlerinde altmışlık sistem (taban 60) kullanılarak kesirler yaygın olarak işlenmiştir.

İrrasyonel sayılar

İrrasyonel sayılar konseptinin kullanıldığına dair kaydedilmiş en eski örnek, M.Ö. 800 ile 500 yılları arasında kaleme alınan Hindistan'a ait 'nda yer almaktadır. İrrasyonel sayıların varoluşuna dair ilk ispatlar, genel kabul görmüş olarak Pisagor'a ve özellikle Pisagorcu Metapontumlu Hippasus'a atfedilmektedir. Hippasus, 2'nin karekökünün irrasyonelliğini kanıtlayan bir çalışma gerçekleştirmiştir, bu çalışmanın büyük olasılıkla geometrik yöntemlerle yapıldığı düşünülmektedir. Rivayete göre, Hippasus 2'nin karekökünü bir kesir olarak temsil etme çabası içindeyken irrasyonel sayıları bulmuştur. Ancak Pisagor, sayıların kesinliğine olan inancı nedeniyle irrasyonel sayıları kabul edememiştir. Onların varlığını mantıksal olarak çürütememiş olmasına rağmen irrasyonel sayıları kabullenememiş ve bu nedenle, iddia edildiği üzere, bu rahatsız edici bilginin yayılmasını önlemek amacıyla Hippasus'u boğarak idam ettirdiği sıkça ileri sürülmüştür.

16. yüzyıl, negatif tam sayılar ve kesirli değerlerin Avrupa matematik topluluğu tarafından sonunda benimsendiği bir dönemi işaret etmektedir. 17. yüzyıla gelindiğinde, ondalık kesirlerin modern notasyonu matematikçiler arasında yaygın bir şekilde kullanılmaya başlanmıştır. Ne var ki, irrasyonel sayıların cebirsel ve aşkınsal bileşenlere ayrılması ve bu sayıların bilimsel olarak incelenmesi 19. yüzyıla dek gerçekleşmemiştir; bu alan, Öklid döneminden itibaren büyük ölçüde atıl kalmıştır. 1872 yılında, Karl Weierstrass, ,Georg Cantor ve Richard Dedekind gibi matematikçilerin teorilerinin yayımlanmasıyla, irrasyonel sayılar üzerine bilimsel çalışmalar yeniden canlanmıştır. , 1869 yılında Heine ile benzer bir başlangıç noktasından hareket etmiş olmasına rağmen, bu teori genellikle 1872 yılına atfedilmektedir. Weierstrass'ın metodolojisi, tarafından 1880 yılında tam anlamıyla ortaya konulmuş, Dedekind'in yaklaşımı ise yazarın sonraki çalışmaları ve Paul Tannery'nin desteğiyle daha da önem kazanmıştır. Weierstrass, Cantor ve Heine, teorilerini sonsuz serilere dayandırırken, Dedekind, gerçek sayılar sisteminde, rasyonel sayıları belirli özelliklere göre iki gruba ayıran bir kesit (Dedekind kesiti) kavramı üzerine kurmuştur. Bu alandaki çalışmalar, Weierstrass, Kronecker, ve Méray gibi matematikçilerin katkılarıyla daha da geliştirilmiştir.

Beşinci derece ve üstü denklemlerin köklerinin aranması, matematikte önemli bir ilerlemeyi temsil etmektedir; Abel-Ruffini teoremi (Ruffini 1799, Abel 1824), bu tür denklemlerin (sadece aritmetik işlemler ve kökler içeren formüller) aracılığıyla çözülemediğini ortaya koymuştur. Dolayısıyla, polinom denklemlerine ait tüm çözümleri kapsayan geniş cebirsel sayılar kümesinin dikkate alınması zorunlu hale gelmiştir. Galois (1832), polinom denklemleri ile grup teorisini bağdaştırarak Galois teorisinin temellerini atmış ve bu alanda yeni bir disiplin yaratmıştır.

, irrasyonel sayılar ile yakın bir ilişkiye sahip olup Cataldi tarafından 1613 yılında tanımlanmıştır; Euler'in çalışmalarıyla ve 19. yüzyılın başında Joseph Louis Lagrange'ın eserleri aracılığıyla bilim dünyasında dikkat çekmiştir. Bu alandaki diğer önemli katkılar, Druckenmüller (1837), Kunze (1857), Lemke (1870) ve Günther (1872) tarafından sağlanmıştır. Ramus, bu konuyu ilk kez determinantlar ile ilişkilendirerek, Heine,Möbius ve Günther'in sonraki katkıları ile birlikte, Kettenbruchdeterminanten teorisinin temelini atmıştır. Bu teori, sürekli kesirlerin matematiksel analizinde önemli bir yere sahiptir ve determinantlar aracılığıyla bu kesirlerin yapısal özelliklerinin incelenmesine olanak tanır.

Aşkınsal (Transendental) sayılar

Aşkınsal (Transendental) sayıların ve reel sayıların mevcudiyeti, tarafından 1844 ve 1851 yıllarında ilk defa ispatlanmıştır. Hermite,, 1873 yılında gerçekleştirdiği çalışmada, e sayısının aşkınsal nitelikte olduğunu ortaya koymuştur ve Lindemann da 1882 yılında π sayısının aşkınsal olduğunu kanıtlamıştır. Cantor ise, reel sayılar kümesinin sayılamaz derecede sonsuz olduğunu, fakat cebirsel sayılar kümesinin sayılabilir derecede sonsuz olduğunu göstererek, sayılamaz derecede sonsuz miktarda aşkınsal sayının var olduğunu ispatlamıştır. Bu bulgular, matematikte aşkınsal sayılar ve reel sayılar teorisinin temel taşlarını oluşturmaktadır.

Sonsuz ve Sonsuzküçükler

Matematiksel sonsuzluk anlayışının en antik örneği, gibi eski bir Hint yazıtında bulunmaktadır. Bu metinde, "Eğer sonsuzluktan bir kısmı çıkartırsanız ya da sonsuzluğa bir kısmı eklerseniz, geriye kalan yine de sonsuz olacaktır." ifadesi yer almaktadır. Sonsuzluk, M.Ö. 400 yıllarında Jain matematikçileri arasında yoğun bir şekilde felsefi bir tartışma konusu olmuştur. Bu matematikçiler, sonsuzluğun beş farklı türünü tanımlamışlardır: tek ve iki yönde sonsuz, alansal olarak sonsuz, her yönden sonsuz ve sürekli olarak sonsuz. Sonsuz bir niceliği ifade etmek için sıklıkla ${\displaystyle {\text{∞}}}$ sembolü kullanılmaktadır.

Aristo, Batı matematiğinin geleneksel sonsuzluk kavramını tanımlamıştır. ile arasında bir ayrım yapmış ve genel olarak sadece sonuncusunun gerçek bir değere sahip olduğu kabul edilmiştir. Galileo Galilei'nin adlı çalışması, sonsuz kümeler arasında birbirine tekabül eden eşlemelerin fikrini ele almıştır. Ancak, teorideki önemli bir sonraki ilerleme Georg Cantor tarafından gerçekleştirilmiştir. Cantor, 1895 yılında yeni küme teorisini konu alan bir eser yayımlamış, bu eserinde transfinite sayılarını tanıtmış ve süreklilik hipotezini formüle etmiştir. Bu çalışmalar, matematikte sonsuzluk teorisinin gelişiminde önemli dönüm noktaları olarak kabul edilir.

1960'larda Abraham Robinson, sonsuz büyüklükteki ve sonsuz küçüklükteki sayıların, standart olmayan analiz alanını geliştirecek şekilde kesin olarak tanımlanabileceği ve kullanılabileceği bir yöntem ortaya koymuştur. sistemi, Isaac Newton ve Gottfried Leibniz'in sonsuz küçük hesaplamalarını icat etmelerinden bu yana matematikçiler, bilim insanları ve mühendisler tarafından yaygın bir şekilde kullanılan sonsuz ve sonsuzküçük sayılarla ilgili fikirleri kesin bir metodoloji çerçevesinde ele alır. Bu sistem, söz konusu kavramların matematikte daha sistematik bir şekilde işlenmesine olanak tanımıştır.

Projektif geometri, sonsuzluğun modern bir geometrik yorumunu sunar ve her bir uzaysal yönde "sonsuzluktaki ideal noktaları" tanımlar. Belirli bir yöndeki paralel çizgi ailelerinin her birinin, ilgili ideal noktaya doğru yakınsaması öngörülür. Bu kavram, perspektif çizimlerdeki kaybolma noktaları fikriyle sıkı bir şekilde bağlantılıdır ve geometrik çizimlerde derinlik ve uzaklık hissi oluşturulmasında temel bir rol oynar.

Karmaşık sayılar

Negatif sayıların kareköklerine dair ilk geçici değinme, İskenderiyeli Heron'nun 1. yüzyılda gerçekleştirdiği çalışmalarda, gerçekleştirilemez bir kesik piramidin hacmini değerlendirirken görülmüştür. Bu konsept, Niccolò Fontana Tartaglia ve Gerolamo Cardano gibi İtalyan matematikçiler tarafından 16. yüzyılda üçüncü ve dördüncü derece polinomların kökleri için kapalı formüllerin keşfedilmesiyle daha da önem kazandı. Bu formüllerin, gerçek çözümlere olan ilgiye rağmen, bazen negatif sayıların kareköklerinin işlenmesini gerektirdiği kısa sürede fark edildi.

Bu durum, negatif sayıların o dönemde bile sağlam bir temele oturtulmamış olması nedeniyle daha da rahatsız ediciydi. René Descartes'ın 1637'de bu nicelikler için "imajiner" terimi türettiğinde, bunu küçümseyici bir niyetle yapmıştı. Karışıklığa neden olan bir diğer faktör, şu denklemin

${\displaystyle \left({\sqrt {-1}}\right)^{2}={\sqrt {-1}}{\sqrt {-1}}=-1}$

cebirsel özdeşlikle keyfi bir şekilde çelişkili görünmesiydi

${\displaystyle {\sqrt {a}}{\sqrt {b}}={\sqrt {ab}},}$

bu, pozitif gerçek sayılar a ve b için geçerlidir ve a, b'den biri pozitif diğeri negatifken karmaşık sayı hesaplamalarında kullanılmıştır. Bu özdeşliğin yanlış kullanımı ve ilgili özdeşlik

${\displaystyle {\frac {1}{\sqrt {a}}}={\sqrt {\frac {1}{a}}}}$

her iki a ve b de negatif olduğunda bile Euler'i zor durumda bırakmıştır. Bu zorluk, Euler'i bu hatadan korumak amacıyla ${\displaystyle {\sqrt {-1}}}$ yerine özel i sembolünü kullanmaya yönlendirir.

18. yüzyıl, Abraham de Moivre ve Leonhard Euler gibi matematikçilerin önemli çalışmalarına sahne oldu. De Moivre'in formülü (1730), aşağıdaki matematiksel ifadeyi ortaya koydu:

${\displaystyle (\cos \theta +i\sin \theta )^{n}=\cos n\theta +i\sin n\theta }$

Öte yandan, karmaşık analiz alanında Euler'in formülü (1748), matematiğe şu önemli eşitliği kazandırdı:

${\displaystyle \cos \theta +i\sin \theta =e^{i\theta }.}$

Bu formüller, trigonometri ve karmaşık sayılar teorisindeki temel ilişkileri kurarak, bu alanlarda derinlemesine çalışmalara olanak tanımıştır.

Karmaşık sayıların mevcudiyeti, 'in 1799 yılında geometrik bir yorumlamayla açıklamasına kadar tam anlamıyla kabul görmemişti. Carl Friedrich Gauss, bu konsepti birkaç yıl sonra yeniden keşfedip popülerleştirdi ve bunun sonucunda karmaşık sayılar teorisi önemli ölçüde genişletildi. Ancak, karmaşık sayıların grafiksel olarak temsil edilme fikri, 'in 1685 yılında yayımlanan De algebra tractatus isimli çalışmasında zaten mevcuttu.

Gauss, aynı yıl içerisinde, karmaşık sayılar alanında her polinomun bu alan içerisinde tam bir çözüm setine sahip olduğunu ispatlayarak, cebirin temel teoremine dair genel kabul görmüş ilk kanıtı ortaya koymuştur. Gauss, a ve b değerlerinin tam sayılar (günümüzde Gauss tam sayıları olarak bilinir) veya rasyonel sayılar olduğu a + bi biçimindeki karmaşık sayıları ele almıştır. Gauss'un öğrencisi ise, ω değerinin x³ − 1 = 0 denkleminin karmaşık bir kökü olduğu a + bω şeklindeki karmaşık sayıları incelemiştir (bu sayılar günümüzde Eisenstein tam sayıları olarak adlandırılır). x^k − 1 = 0 denkleminden türetilen birlik kökleri için k değerinin yüksek olduğu durumlar için tanımlanan diğer karmaşık sayı sınıfları (döngüsel alanlar olarak adlandırılır), karmaşık sayılar alanındaki bu genişlemeye katkıda bulunmuştur. Bu genelleme, büyük ölçüde 'a aittir; Kummer, ideal sayıları da icat etmiş olup, bu sayılar 1893 yılında Felix Klein tarafından geometrik nesneler olarak tanımlanmıştır.

1850 yılında , karmaşık sayılar teorisinde önemli bir gelişmeye imza atarak kutuplar ile dalga kırılma noktaları arasındaki farkı belirginleştirdi ve matematiksel tekilliklerin temelini oluşturan esas tekillik noktaları kavramını ortaya koydu. Bu yaklaşım, genişletilmiş karmaşık düzlem kavramının temellerinin atılmasına önayak oldu.

Asal sayılar

Asal sayılar, kayıtlı tarihin her evresinde araştırma konusu olmuştur. Bunlar, yalnızca 1 ve kendileri ile bölünebilme özelliğine sahip pozitif tam sayılardır. Öklid, Elementler adlı eserinin bir bölümünü asal sayılar teorisine adamıştır; bu bölümde, asal sayıların sonsuz olduğunu ve aritmetiğin temel teoremini ispatlamış, aynı zamanda iki sayının en büyük ortak bölenini bulmak için Öklid algoritmasını tanıtmıştır.

M.Ö. 240 yılında, Eratosthenes, asal sayıları etkin bir şekilde saptamak için Eratosten kalburu yöntemini kullanmıştır. Ancak, asal sayılar teorisindeki önemli gelişmelerin çoğu, Avrupa'da Rönesans dönemi ve sonrasına aittir.

1796 yılında Adrien-Marie Legendre, asal sayıların asimptotik dağılımını açıklayan asal sayı teoremini tahmin etmiştir. Asal sayıların dağılımı ile ilgili diğer önemli bulgular arasında, Euler'in asal sayıların karşılıklı değerlerinin toplamının diverjansını ispatlaması ve herhangi bir yeterince büyük çift sayının iki asal sayının toplamı şeklinde ifade edilebileceğini öne süren Goldbach varsayımı yer almaktadır. Asal sayıların dağılımı ile ilgili bir diğer önemli varsayım ise, Bernhard Riemann tarafından 1859 yılında formüle edilen Riemann hipotezidir. Asal sayı teoremi, Jacques Hadamard ve tarafından 1896 yılında kanıtlanmıştır. Goldbach ve Riemann'ın varsayımları ise hâlâ ne kanıtlanmış ne de çürütülmüştür.

Sınıflandırma

Sayılar, doğal sayılar ve reel sayılar gibi, 'sayı kümeleri' veya 'sayı sistemleri' adı verilen matematiksel kümeler içerisinde sınıflandırılabilir. Temel sayı sistemleri aşağıdaki gibidir:

Temel sayı sistemleri

${\displaystyle \mathbb {N} }$	Doğal sayılar	0, 1, 2, 3, 4, 5, ... or 1, 2, 3, 4, 5, ... ${\displaystyle \mathbb {N} _{0}}$ veya ${\displaystyle \mathbb {N} _{1}}$ kullanılır.
${\displaystyle \mathbb {Z} }$	Tam sayılar	..., −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, ...
${\displaystyle \mathbb {Q} }$	Rasyonel sayılar	a/b'da a ve b tam sayı ve b != 0
${\displaystyle \mathbb {R} }$	Reel sayılar	Rasyonel sayılardan oluşan bir yakınsak dizinin limit değeri
${\displaystyle \mathbb {C} }$	Karmaşık sayılar	a + bi şeklinde ifade edilen, burada a ve b reel sayılar olup, i ise -1'in formal karekökünü temsil eder

Bu sayı sistemlerinden her biri, bir sonraki sayı sisteminin alt kümesini oluşturur. Dolayısıyla, bir rasyonel sayının aynı zamanda bir reel sayı olduğu ve her reel sayının da bir karmaşık sayı olduğu söylenebilir. Bu durum sembolik olarak şu şekilde gösterilebilir:

${\displaystyle \mathbb {N} \subset \mathbb {Z} \subset \mathbb {Q} \subset \mathbb {R} \subset \mathbb {C} }$.

Bir tablo olarak sayılar için şöyle sınıflandırma yapılabilir:

${\displaystyle \scriptstyle \mathbb {C} {\mbox{ Karmaşık}}{\begin{cases}\scriptstyle \mathbb {R} &{\mbox{Gerçek}}{\begin{cases}\scriptstyle \mathbb {Q} &{\mbox{Rasyonel}}{\begin{cases}\scriptstyle \mathbb {Z} &{\mbox{Tam sayılar}}{\begin{cases}\scriptstyle \mathbb {N} &{\mbox{Doğal Sayılar}}\\\end{cases}}\\&{\mbox{Oranlı}}\end{cases}}\\&{\mbox{İrrasyonel}}\end{cases}}\\jjj&{\mbox{Sanal}}\end{cases}}}$

Aşağıdaki diyagramda, sayı kümelerine ilişkin daha kapsamlı bir listeleme yer almaktadır.

Sayı sistemleri Karmaşık ${\displaystyle :\;\mathbb {C} }$ Reel ${\displaystyle :\;\mathbb {R} }$ Rasyonel ${\displaystyle :\;\mathbb {Q} }$ Tam sayı ${\displaystyle :\;\mathbb {Z} }$ Doğal ${\displaystyle :\;\mathbb {N} }$ Sıfır: 0 Bir: 1 Asal sayılar Bileşik sayılar Negatif tam sayılar Kesir Devirli ondalık sayı İrrasyonel Cebirsel irrasyonel Aşkın Sanal

Sayma sayılar

Sayma sayıları boştan farklı bir kümenin elemanlarını azlık veya çokluk yönünden nitelemekten ziyade onların içindeki eleman miktarına göre verilen bir temsilciler kümesi olarak tanımlanır. Temsilcilere verilen isme kanonik temsilci denir. Her sayma sayısı aynı zamanda bir kanonik temsilcidir. Sayma sayılarına sıfırın dahil olmamasının sebebi boş kümenin içinde temsil edecek bir elemanın olmamasıdır.

${\displaystyle \scriptstyle \mathbb {N} ^{+}=\left\{1,2,3,...\right\}}$

Doğal sayılar

1'den itibaren doğal sayılar

Doğal sayılar 0'dan başlayarak sonsuza kadar giden sayılardır. Matematikte doğal sayılar kümesi 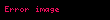${\displaystyle \scriptstyle \mathbb {N} }$ ile gösterilir. Doğal sayılar ismi bu sayıların doğada görüp tanıdığımız sayılar olduğu fikrinden ileri gelmektedir. Doğal sayılar kümesi "0" ve pozitif tüm tam sayıların olduğu kümedir.

${\displaystyle \scriptstyle \mathbb {N} =\{0,1,2,3,4,5,6,7,...\}}$

0 sayısı, Antik Yunan döneminde dahi sayı olarak kabul edilmezdi. Ancak 19. yüzyılda, küme teorisyenleri ve diğer matematikçiler, 0'ı (boş kümenin kardinalitesi, yani 0 eleman, bu nedenle 0 en küçük kardinal sayı olarak kabul edilir) doğal sayılar kümesine dahil etmeye başladılar. Günümüzde, matematikçilerin farklı yaklaşımları neticesinde, terim hem 0'ı içeren hem de içermeyen sayı kümelerini tanımlamak için kullanılmaktadır. Tüm doğal sayılar kümesini ifade etmek için kullanılan matematiksel sembol N olup, ${\displaystyle \mathbb {N} }$ şeklinde gösterilir ve kümenin 0 ile mi yoksa 1 ile mi başlayacağını belirtmek amacıyla ${\displaystyle \mathbb {N} _{0}}$ veya ${\displaystyle \mathbb {N} _{1}}$ şeklinde ifade edilir.

Onlu sayı sistemi, günümüzde matematiksel işlemler için yaygın olarak kullanılan sistem olup, doğal sayıların gösterimi için on adet sayısal basamak kullanır: 0, 1, 2, 3, 4, 5, 6, 7, 8 ve 9. Radiks veya taban, bir sayı sisteminin sayıları ifade etmek için kullandığı, sıfır dahil olmak üzere, benzersiz sayısal basamakların toplam sayısını belirtir (ondalık sistem için bu değer 10'dur). Bu onlu taban sistemde, bir doğal sayının en sağdaki basamağının basamak değeri 1 olup, diğer basamakların her birinin basamak değeri, hemen sağında yer alan basamağın basamak değerinin on katı kadar olur.

Küme teorisi, modern matematiğin aksiyomatik bir temeli olarak görev yapabilir ve bu çerçevede, doğal sayılar, eşit büyüklükteki kümelerin sınıflandırılması yoluyla ifade edilebilir. Mesela, 3 sayısı, tam olarak üç öğeye sahip olan tüm kümelerin bir sınıfı olarak ifade edilebilir. Diğer bir yöntem olarak, Peano Aritmetiği'nde 3 sayısı, sss0 olarak gösterilir; burada 's', "ardıl" fonksiyonunu temsil eder (bu bağlamda 3, 0 sayısının üçüncü ardılı olarak kabul edilir). 3 sayısını formel olarak ifade etmek için birçok farklı yöntem mevcuttur; tek gereken, belirli bir sembolü veya sembol dizisini üç defa işaretlemektir.

Tam sayılar

Tam sayılar eksi sonsuzdan artı sonsuza kadar giderler. Yani "0"ın iki yanından sonsuza kadar uzanırlar. Tam sayılar kümesi ${\displaystyle \scriptstyle \mathbb {Z} }$ ile gösterilir. Buradaki Z harfi, Almanca 'Zahl' (sayı) kelimesinden türemiştir.

${\displaystyle \scriptstyle \mathbb {Z} =\{...,-4,-3,-2,-1,0,1,2,3,...\}}$

Pozitif tam sayılar

Başında "+" işareti bulunan veya bir şey bulunmayan tam sayılar pozitif tam sayılar adını alırlar. Sayı ekseninde (sayı doğrusunda) 0'ın sağ yanında yer alırlar. Tüm sayma sayıları pozitif tam sayılardır. Pozitif tam sayılar kümesi ${\displaystyle \scriptstyle \mathbb {Z} ^{+}}$ ile gösterilir ve aşağıdaki gibi tanımlıdır:

${\displaystyle \scriptstyle \mathbb {Z} ^{+}=\{+1,+2,+3,+4,+5...\}}$

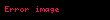
Negatif tam sayılar

Başında "-" işareti olan tam sayılar negatif tam sayılar adını alırlar. Sayı ekseninde 0'ın sol yanında yer alırlar. Negatif tam sayılar kümesi ${\displaystyle \scriptstyle \mathbb {Z} ^{-}}$ ile gösterilir. Cebirde çıkarma işlemi bu sayıların diğer tam sayılarla toplanması olarak ifade edilir.

${\displaystyle \scriptstyle \mathbb {Z} ^{-}=\{...,-3,-2,-1\}}$

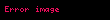
Sıfır

Tam sayıdır. Sıfır (0) negatif veya pozitif bir tam sayı değildir. Bir uzlaşma noktasıdır. Bu iki kümeden herhangi birinde yer almaz. Ancak tam sayılar aşağıdaki gibi de tanımlanabilir:

${\displaystyle \scriptstyle \mathbb {Z} =\scriptstyle \mathbb {Z} ^{-}\cup \{0\}\cup \scriptstyle \mathbb {Z} ^{+}}$

Sıfırın doğal sayı kabul edilmediği (akademik) çevreler azımsanmayacak kadar fazladır. Sıfırı dahil eden çevreler doğal sayılar kümesini ${\displaystyle \scriptstyle \mathbb {N} _{(0)}}$ sembolü ile gösterirler, sıfırı dahil etmeyen çevrelerse sıfırın dahil olmadığı sayma sayıları kümesini ${\displaystyle \scriptstyle \mathbb {N} ^{+}}$ ile gösterirler.

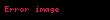
Rasyonel sayılar

Bir rasyonel sayı, tam sayı bir pay ve pozitif tam sayı bir payda ile ifade edilebilen bir kesir olarak tanımlanır. Negatif paydalar kullanılabilir ancak her rasyonel sayı pozitif bir payda ile eşit olduğundan, genellikle bu durumdan kaçınılır. Kesirler, pay ve payda olarak iki tam sayı ile ifade edilir ve bu iki sayı arasında bir bölme işareti bulunur. m/n kesri, n eşit parçaya bölünmüş bir bütünün m parçasını ifade eder. Farklı iki kesir, aynı rasyonel sayıyı temsil edebilir; örneğin 1/2 ile 2/4 birbirine eşittir, yani:

${\displaystyle {1 \over 2}={2 \over 4}.}$

Genel bir ifade ile,

${\displaystyle {a \over b}={c \over d}}$, sadece ve sadece ${\displaystyle {a\times d}={c\times b}.}$ olduğunda geçerlidir.

Eğer m sayısının mutlak değeri, pozitif kabul edilen n sayısından daha büyükse, kesirin mutlak değeri 1'den fazla olacaktır. Kesirler, 1'e göre büyük, küçük veya ona eşit olabilirler; ayrıca pozitif, negatif veya 0 değerlerini alabilirler. Tüm rasyonel sayılar kümesi, her bir tam sayının paydası 1 olarak belirlenebilen bir kesir biçiminde ifade edilebildiği için, tam sayıları da kapsar. Örnek olarak −7 sayısı, −7/1 şeklinde ifade edilebilir. Rasyonel sayılar için kullanılan sembol 'Q'dur (quotient, yani bölüm kelimesinden gelir) ve ${\displaystyle \mathbb {Q} }$ şeklinde de gösterilir.

Reel sayılar

İrrasyonel sayılar kümesi ile rasyonel sayılar kümesinin birleşimi gerçek sayılar kümesini oluşturur. Bu kümeye reel sayılar veya gerçek sayılar da denir.

Reel sayılar için kullanılan sembol 'R'dir ve ${\displaystyle \mathbb {R} }$ şeklinde de ifade edilir. Bu sembol, ölçümle ilgili tüm sayıları kapsar. Her bir reel sayı, sayı doğrusu üzerinde belirli bir noktayla ilişkilendirilir. İzleyen metin, özellikle pozitif reel sayılar üzerine yoğunlaşacaktır. Negatif reel sayıların işlenişi, aritmetik kuralların genel prensipleri çerçevesinde gerçekleştirilir ve bunların gösterimi, karşılık gelen pozitif sayının önüne eksi işareti eklenerek yapılır, mesela -123.456.

Birçok reel sayı, ancak ondalık sayılar aracılığıyla yaklaşık bir biçimde temsil edilebilir; bu durumda ondalık nokta, birler basamağındaki rakamın hemen sağ tarafına konumlandırılır. Ondalık noktasının sağ tarafında yer alan her bir rakam, solundaki rakamın basamak değerinin onda birine eşit bir değere sahiptir. Mesela, 123.456 sayısı, 123456/1000 olarak ifade edilir ki bu, yüz iki on, üç bir, dört ondalık, beş yüzdelik ve altı binde bir anlamına gelir. Bir reel sayı, yalnızca rasyonel ise ve onun kesirli kısmı, 2 veya 5 sayılarının asal çarpanlarını içeren bir paydaya sahipse, sınırlı sayıda ondalık basamak ile ifade edilebilir. Bu sayılar, ondalık sistemdeki taban olan 10'un asal çarpanlarıdır. Örneğin, bir yarım için 0.5, bir beşte bir için 0.2, bir onda bir için 0.1 ve bir elli de bir için 0.02 değerleri kullanılır. Diğer reel sayıları ondalık olarak ifade etmek, ondalık noktasının sağ tarafında sonsuz bir rakam dizisi gerektirecektir. Eğer bu sonsuz rakam dizisi belli bir deseni izliyorsa, bu desen üç nokta veya deseni gösteren diğer bir gösterim ile ifade edilebilir. Bu tür bir ondalık sayıya 'tekrar eden ondalık' denir. Bu bağlamda, 1/3 sayısı, desenin sürekliliğini belirten üç nokta ile 0.333... şeklinde ifade edilir. Sürekli tekrar eden 3'ler ayrıca 0.3 şeklinde de gösterilir.

Bu tekrar eden ondalık sayılar (sıfırların yeniden oluşumu dahil), rasyonel sayıları kesinlikle belirtir; yani, her rasyonel sayı reel bir sayıdır ancak her reel sayının rasyonel olması gerekmez. Rasyonel olmayan reel sayılara irrasyonel sayı adı verilir. Tanınmış irrasyonel gerçek sayılardan biri, herhangi bir dairenin çevresinin çapına oranı olan π sayısıdır. Pi, bazen

${\displaystyle \pi =3.14159265358979\dots ,}$

şeklinde ifade edildiğinde, noktalı virgül, ondalık kısmın tekrar ettiğini değil, ondalık kısmın sonunun olmadığını gösterir. π sayısının irrasyonel olduğu ispatlanmıştır. İrrasyonel bir reel sayı olduğu ispatlanan diğer bir ünlü sayı,

${\displaystyle {\sqrt {2}}=1.41421356237\dots ,}$

2'nin kareköküdür, yani karesi 2 olan benzersiz pozitif gerçek sayıdır. Bu iki sayı, trilyonlarca ( 1 trilyon = 10¹² = 1,000,000,000,000 ) basamağa kadar (bilgisayar yardımıyla) yaklaşık olarak hesaplanmıştır.

Bu belirgin örneklerin yanı sıra, reel sayıların neredeyse tamamı irrasyonel niteliktedir ve bu sebepten ötürü tekrar eden desenlere sahip değillerdir, bu yüzden bunlara karşılık gelen ondalık gösterimleri de mevcut değildir. Bu sayılar, yalnızca ondalık gösterimlerle yaklaşık bir şekilde temsil edilebilirler; bu, yuvarlanmış ya da kesilmiş reel sayıları ifade eder. Herhangi bir yuvarlanmış veya kesilmiş sayı doğası gereği bir rasyonel sayıdır ve bunlardan yalnızca sayılabilir derecede çoklukta bulunur. Ölçümlerin tümü, doğaları gereği yaklaşık değerlerdir ve daima bir hata marjına sahiptirler. Bu çerçevede, 123.456 sayısı, 1234555/10000'den büyük veya eşit ve 1234565/10000'den kesinlikle küçük olan herhangi bir gerçek sayı için bir yaklaşık olarak kabul edilir (3 ondalık basamağa yuvarlama); ya da 123456/1000'den büyük veya eşit ve 123457/1000'den kesinlikle küçük olan herhangi bir reel sayı için bir yaklaşık olarak kabul edilir (3. ondalık basamağın ardından kesme). Ölçümün kendisi kadar hassasiyeti öneren rakamlar elenmelidir. Kalan rakamlar, o zaman önemli rakamlar olarak adlandırılır. Örneğin, bir cetvel ile yapılan ölçümler genellikle en az 0.001 metre hata payı olmaksızın gerçekleştirilemez. Eğer bir dikdörtgenin kenarları 1.23 m ve 4.56 m olarak ölçülürse, çarpım sonucunda dikdörtgenin alanı için 5.614591 m² ile 5.603011 m² arasında bir değer elde edilir. Ondalık noktasından sonra ikinci basamak bile korunmadığı için, sonraki basamaklar önemli kabul edilmez. Bu sebeple, sonuç genelde 5.61 olarak yuvarlanır.

Aynı kesir birden fazla şekilde ifade edilebildiği gibi, aynı reel sayının da birden fazla ondalık gösterimi mümkündür. Örnek olarak, 0.999..., 1.0, 1.00, 1.000, ..., hepsi 1 doğal sayısını ifade eder. Bir reel sayı için mümkün olan ondalık gösterimler; belirli bir ondalık basamağına kadar olan bir yaklaşım, sınırsız sayıda ondalık basamağı boyunca devam eden bir desenin oluşturulduğu bir yaklaşım veya yalnızca sonlu sayıda ondalık basamağı içeren bir kesin değer şeklinde olabilir. Bu son durumda, son sıfır olmayan basamak, bir altındaki rakam ile değiştirilip ardından sınırsız sayıda 9 eklenerek veya son sıfır olmayan basamağın ardından sınırsız sayıda 0 eklenerek de ifade edilebilir. Dolayısıyla, kesin bir gerçek sayı olan 3.74, aynı zamanda 3.7399999999... ve 3.74000000000.... olarak da ifade edilebilir. Benzer biçimde, sınırsız sayıda 0 içeren bir ondalık sayı, sağdaki en uçtaki sıfır olmayan basamağın sağında yer alan 0'lar çıkarılarak; sınırsız sayıda 9 içeren bir ondalık sayı ise, 9'dan küçük olan en sağdaki basamağın bir artırılması ve bu basamağın sağında yer alan tüm 9'ların 0'a dönüştürülmesiyle yeniden yazılabilir. Son olarak, bir ondalık noktasının sağındaki sınırsız 0 dizisi göz ardı edilebilir. Örneğin, 6.849999999999... = 6.85 ve 6.850000000000... = 6.85 olarak kabul edilir. Eğer bir sayısal ifadedeki tüm rakamlar 0 ise, bu sayı 0 olarak kabul edilir ve eğer bir sayısal ifadedeki tüm rakamlar bitmeyen bir 9 dizisinden oluşuyorsa, ondalık noktasının sağındaki dokuzlar ihmal edilip, ondalık noktasının solundaki 9 dizisine bir eklenerek ifade edilebilir. Mesela, 99.999... = 100 olarak kabul edilir.

Reel sayılar, olarak bilinen ancak oldukça teknik düzeyde bir özelliğe sahiptir. Bir , reel sayıların özelliğine de sahip olduğu ispatlandığında, bu alanın gerçek sayılarla izomorf olduğu ortaya konabilir. Fakat, gerçek sayılar ${\displaystyle x^{2}+1=0}$ cebirsel denkleminin bir çözümünü (çoğunlukla eksi birin karekökü olarak ifade edilir) içermedikleri için, oluşturmazlar.

Karmaşık sayılar

Daha yüksek bir soyutlama düzeyine geçildiğinde, reel sayılar, karmaşık sayılara genişletilebilir. Bu sayılar kümesi, tarih boyunca kübik ve kuadratik polinomların köklerine ilişkin kapalı formüllerin araştırılması sürecinde gelişmiştir. Bu arayış, negatif sayıların kareköklerini içeren ifadelere ve sonuç olarak -1 sayısının karekökü olan yeni bir sayının tanımına yol açmıştır; bu sayı, Leonhard Euler tarafından i olarak sembolize edilen ve hayali birim olarak adlandırılan bir birimdir. Karmaşık sayılar, a ve b reel sayıları olmak üzere, ${\displaystyle a+bi}$ biçimindeki tüm sayıları kapsar. Bu bağlamda, karmaşık sayılar, iki gerçek boyutlu bir vektör uzayı olan karmaşık düzlem üzerinde noktalara denk gelir. a + bi ifadesinde a, gerçek kısmı ve b, hayali kısmı temsil eder. Bir karmaşık sayının gerçek kısmı 0 ise, bu sayı hayali sayı olarak adlandırılır veya tamamen hayali olarak nitelendirilir; hayali kısmı 0 ise, bu sayı bir gerçek sayıdır. Böylelikle, reel sayılar karmaşık sayıların bir alt kümesini oluşturur. Eğer bir karmaşık sayının gerçek ve hayali kısımları tam sayı ise, bu sayı olarak isimlendirilir. Karmaşık sayılar için kullanılan sembol, 'C' veya ${\displaystyle \mathbb {C} }$'dir.

Cebirin temel teoremi, karmaşık sayıların cebirsel olarak kapalı bir alan oluşturduğunu, yani karmaşık katsayılara sahip her polinomun karmaşık sayılar içinde bir kökü olduğunu ifade eder. Gerçek sayılar gibi, karmaşık sayılar da bir alan oluşturur ve bu alan tamdır; fakat gerçek sayılardan farklı olarak sıralı değildir. Yani, inin 1'den büyük olduğunu ya da inin 1'den küçük olduğunu ifade etmenin tutarlı bir anlamı yoktur. Teknik bir dille ifade edilecek olursa, karmaşık sayılar, alan işlemleriyle uyumlu bir total sıralamadan yoksundur.

Tam sayıların alt kategorileri

Çift ve tek sayılar

Bir çift sayı, iki sayısına tam olarak bölünebilen ve böylece kalan bırakmayan bir tam sayıdır; buna karşılık, bir tek sayı çift olmayan tam sayılardır. Günümüzde "tam bölünebilir" şeklindeki eski usul ifade, genellikle "bölünebilir" şeklinde kısaltılarak kullanılmaktadır. Herhangi bir tek sayı n, uygun bir k tam sayısı için n = 2k + 1 formülü ile ifade edilebilir. k = 0 ile başlandığında, ilk negatif olmayan tek sayılar {1, 3, 5, 7, ...} olarak sıralanır. Her çift sayı m, yine bir tam sayı olan k için m = 2k şeklinde ifade edilebilir. Benzer biçimde, ilk negatif olmayan çift sayılar {0, 2, 4, 6, ...} olarak belirlenir.

Asal sayılar

Bir asal sayı, genellikle sadece asal olarak kısaltılan, 1'den büyük ve iki daha küçük pozitif tam sayının çarpımı olmayan bir tam sayıdır. İlk birkaç asal sayı 2, 3, 5, 7 ve 11'dir. Çift ve tek sayılar için mevcut olan basit formüllerin aksine, asal sayıları türetecek bir formül bulunmamaktadır. Asal sayılar üzerine 2000 yıldan fazla süredir yapılan geniş çaplı çalışmalar, çeşitli soruları gündeme getirmiş, bunların yalnızca bir kısmına yanıt bulunabilmiştir. Bu tür soruların ele alınışı, sayılar teorisi disiplinine aittir. , halen yanıtlanmamış sorulardan birine örnek teşkil eder: "Her çift sayı, iki asal sayının toplamı mıdır?"

Bir'den büyük her tam sayının, asal sayıların çarpımı olarak yalnızca tek bir yolda ifade edilebileceği, asal sayıların yeniden düzenlenmesi dışında, sorusuna verilen yanıt doğrulanmıştır; bu ispatlanmış iddia, aritmetiğin temel teoremi olarak bilinir. Bir kanıt, Öklid'in Elementleri eserinde sunulmuştur.

Diğer tam sayı sınıfları

Doğal sayıların çeşitli alt kümeleri, belirli çalışmaların odak noktası olmuş ve çoğunlukla bu sayılar üzerine çalışmalar yapan ilk matematikçinin adıyla anılmıştır. Fibonacci sayıları ve mükemmel sayılar gibi tam sayı kümeleri, bu tür örnekler arasında yer alır. Daha fazla örnek için ardışık sayılar maddesine başvurulabilir.

Karmaşık Sayıların alt kategorileri

Cebirsel, İrrasyonel ve Transandantal sayılar

Tam sayı katsayılarına sahip bir polinom denkleminin çözümü olan sayılar, cebirsel sayı olarak adlandırılır. Rasyonel sayılar dışındaki reel sayılara irrasyonel sayı adı verilir. Cebirsel olmayan karmaşık sayılarsa transandantal sayı olarak tanımlanır. Tam sayı katsayılı monik polinom denkleminin çözümleri olan cebirsel sayılar, olarak isimlendirilir.

İnşa-edilebilir sayılar

Pergel ve çizgilik çizimleri çalışmalarının klasik sorunlarından esinlenilerek, birim uzunluktaki belirli bir segmentten başlayarak, perge ve çember kullanılarak sonlu adımlarda inşa edilebilen karmaşık sayıların gerçek ve sanal kısımlarına sahip sayılar, olarak tanımlanır.

Hesaplanabilir sayılar

Bir hesaplanabilir sayı, aynı zamanda rekürsif sayı olarak da tanımlanan, belirli bir pozitif n değeri verildiğinde, hesaplanabilir sayının ondalık gösterimindeki ilk n rakamı üretebilen bir algoritmanın mevcut olduğu bir reel sayıdır. Eş değer tanımlamalar, , Turing makinesiler veya λ-hesaplaması aracılığıyla yapılabilir. Hesaplanabilir sayılar, bir polinomun köklerinin elde edilmesi de dahil olmak üzere, tüm standart aritmetik işlemler açısından stabil olup, reel cebirsel sayıları içeren bir gerçek kapalı alan oluşturur.

Hesaplanabilir sayılar, bir bilgisayarda kesin bir şekilde ifade edilebilecek reel sayılar olarak değerlendirilebilir: bir hesaplanabilir sayı, ilk rakamları ve daha fazla rakamı hesaplamak üzere tasarlanmış bir program ile kesin bir şekilde belirlenir. Ancak, hesaplanabilir sayılar pratikte nadiren tercih edilir. Bunun bir sebebi, iki hesaplanabilir sayının eşitliğinin test edilmesi için bir algoritmanın bulunmamasıdır. Daha net bir ifadeyle, herhangi bir hesaplanabilir sayıyı girdi olarak kabul eden ve bu sayının sıfıra eşit olup olmadığını her durumda belirleyebilecek bir algoritma mevcut olamaz.

Hesaplanabilir sayılar kümesi, doğal sayılarla aynı kardinaliteye sahiptir. Bu nedenle, neredeyse tüm reel sayılar hesaplanabilir değildir. Yine de, hesaplanabilir olmayan bir reel sayıyı açıkça belirlemek büyük bir zorluk teşkil eder.

Kavram uzantıları

0'dan 100'e kadar asal ve bileşik sayılar. Asal sayılar Bileşik sayılar 0 ve 1

p-adik sayılar

p-adik sayılar, reel sayıların ondalık noktasının sağında sonsuza kadar uzayabilen uzantılara sahip olabileceği gibi, ondalık noktasının solunda da sonsuz uzunlukta genişlemelere sahip olabilir. Sonuçlanan sayı sistemi, basamaklar için hangi tabanın kullanıldığına bağlıdır: herhangi bir taban mümkündür, ancak bir asal sayı tabanı en iyi matematiksel özellikleri sağlar. p-adik sayılar kümesi, rasyonel sayıları içerir, ancak karmaşık sayıların içinde yer almaz.

Bir sonlu alan üzerindeki bir elemanları ve cebirsel sayılar birçok benzer özelliğe sahiptir. Bu nedenle, sayılar teorisyenleri tarafından sıklıkla sayılar olarak kabul edilirler. p-adik sayılar, bu analojide önemli bir rol oynar.

Hiperkompleks sayılar

Karmaşık sayıların içinde yer almayan bazı sayı sistemleri, karmaşık sayıların inşasını genelleştirerek reel sayılardan türetilebilir. Bunlar bazen olarak adlandırılır. Bunlara, çarpma işleminin değişmeli olmayan olduğu Sir William Rowan Hamilton tarafından tanıtılan dördeyler H, çarpmanın ek olarak değişmeli olmadığı ve çarpmanın ne , ne de değişmeli olduğu dahildir.

Transfinite sayılar

Sonsuz kümelerle başa çıkmak için, doğal sayılar ardışık sayılar ve kardinal sayılar olarak genelleştirilmiştir. İlki kümenin sıralamasını verirken, ikincisi boyutunu verir. Sonlu kümeler için, hem sıralı hem de kardinal sayılar doğal sayılarla özdeşleştirilir. Sonsuz durumda, birçok sıralı sayı aynı kardinal sayıya karşılık gelir.

Standart olmayan sayılar

, kullanılır. Hipergerçekler veya standart olmayan gerçekler (genellikle *R olarak gösterilir), reel sayılar R'nin sıralı alanının uygun bir olan ve sağlayan bir ifade eder. Bu ilke, R hakkındaki doğru ifadelerin *R hakkında doğru birinci dereceden ifadeler olarak yeniden yorumlanmasına izin verir.

ve , sonsuzküçük sayılar ve sonsuzbüyük sayılar ekleyerek reel sayıları genişletir, ancak yine de alanlar oluşturur.

Sayı (dilbilim)

Dilbilim alanında sayılar ya da sayı adları, biçimbilimsel (morfolojik) olarak bağımsız bir sözcük kategorisidir.

Türkçede sayı türleri

• asal sayılar (iki, üç,beş, yedi ...)
• sıra sayıları (onuncu, yüzüncü ...)
• üleştirme sayıları (ikişer, onar ...)
• kesir sayıları (beşte bir ...)

Sayı sıfatı

Dilbilimde, sayı kavramı içeren sıfatlara sayı sıfatı denir (örneğin on yıl, ikinci gün, birer kişi dizimlerindeki on, ikinci, birer sözcükleri).

Ayrıca bakınız

• Matematiksel sabit
• Karmaşık sayılar
• Büyüklük mertebesi
• Fiziksel sabit
• Fiziksel nicelik
• Basamak
• Asal sayı
• Skaler

Notlar

1. ^ . OED Çevrimiçi (İngilizce). Oxford University Press. 4 Ekim 2018 tarihinde kaynağından arşivlendi. Erişim tarihi: 16 Mayıs 2017. 
2. ^ . OED. Oxford University Press. 30 Temmuz 2022 tarihinde kaynağından arşivlendi. Erişim tarihi: 16 Mayıs 2017. 
3. ^ Matson, John. . Scientific American (İngilizce). 26 Ağustos 2017 tarihinde kaynağından arşivlendi. Erişim tarihi: 16 Mayıs 2017. 
4. ^ ^{a b} Hodgkin, Luke (2 Haziran 2005). (İngilizce). OUP Oxford. ss. 85-88. ISBN . 4 Şubat 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 16 Mayıs 2017. 
5. ^ Mathematics across cultures : the history of non-western mathematics. Dordrecht: Kluwer Academic. 2000. ss. 410-411. ISBN . 
6. ^ Descartes, René (1954). La Géométrie: René Descartes'ın Geometrisi ve İlk Baskının Faksimilesi. Dover Publications. ISBN . Erişim tarihi: 20 Nisan 2011. 
7. ^ ^{a b} Gilsdorf, Thomas E. (2012). Introduction to cultural mathematics : with case studies in the Otomies and the Incas (İngilizce). Hoboken, N.J.: Wiley. ISBN . OCLC 793103475. 
8. ^ Restivo, Sal P. (1992). Mathematics in society and history : sociological inquiries (İngilizce). Dordrecht. ISBN . OCLC 883391697. 
9. ^ ^{a b} Ore, Øystein (1988). Number theory and its history (İngilizce). New York: Dover. ISBN . OCLC 17413345. 
10. ^ Gouvêa, Fernando Q. , II.1 Bölümü, "The Origins of Modern Mathematics", s. 82. Princeton University Press, 28 Eylül 2008. . "Today, it is no longer that easy to decide what counts as a 'number.' The objects from the original sequence of 'integer, rational, real, and complex' are certainly numbers, but so are the p-adics. The quaternions are rarely referred to as 'numbers,' on the other hand, though they can be used to coordinatize certain mathematical notions."
11. ^ Marshack, Alexander (1971). The roots of civilization; the cognitive beginnings of man's first art, symbol, and notation (İngilizce) ([1. baskı] bas.). New York: McGraw-Hill. ISBN . OCLC 257105. 
12. ^ (İngilizce). Math.buffalo.edu. 7 Nisan 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 30 Ocak 2012. 
13. ^ Chrisomalis, Stephen (1 Eylül 2003). "The Egyptian origin of the Greek alphabetic numerals". Antiquity (İngilizce). 77 (297). ss. 485-96. doi:10.1017/S0003598X00092541. ISSN 0003-598X. 
14. ^ ^{a b} Bulliet, Richard; Crossley, Pamela; Headrick, Daniel; Hirsch, Steven; Johnson, Lyman (2010). (İngilizce). Cengage Learning. s. 192. ISBN . 28 Ocak 2017 tarihinde kaynağından arşivlendi. Erişim tarihi: 16 Mayıs 2017. Indian mathematicians invented the concept of zero and developed the "Arabic" numerals and system of place-value notation used in most parts of the world today. 
15. ^ . Sunsite.utk.edu. 26 Nisan 1999. 12 Ocak 2012 tarihinde kaynağından arşivlendi. Erişim tarihi: 30 Ocak 2012. 
16. ^ Sánchez, George I. (1961). Arithmetic in Maya (İngilizce). Austin, Teksas. 
17. ^ Staszkow, Ronald; Robert Bradshaw (2004). The Mathematical Palettei (3. baskı) (İngilizce). Brooks Cole. s. 41. ISBN . 
18. ^ Smith, David Eugene (1958). History of Modern Mathematics (İngilizce). Dover Yayınları. s. 259. ISBN . 
19. ^ (İngilizce). 4 Mayıs 2022 tarihinde kaynağından arşivlendi. Erişim tarihi: 4 Mayıs 2022. 
20. ^ Selin, Helaine (2000). Mathematics across cultures: the history of non-Western mathematics (İngilizce). Kluwer Akademik Yayıncılar. s. 451. ISBN . 
21. ^ Bernard Frischer (1984). "Horace and the Monuments: A New Interpretation of the Archytas Ode". D.R. Shackleton Bailey (Ed.). Harvard Studies in Classical Philology (İngilizce). Harvard University Press. s. 83. ISBN . 
22. ^ Eduard Heine, "Die Elemente der Functionenlehre", [Crelle's] Journal für die reine und angewandte Mathematik, No. 74 (1872): 172–188.
23. ^ Georg Cantor, "Ueber unendliche, lineare Punktmannichfaltigkeiten", pt. 5, Mathematische Annalen, 21, 4 (1883‑12): 545–591.
24. ^ Richard Dedekind, Stetigkeit & irrationale Zahlen 9 Temmuz 2021 tarihinde Wayback Machine sitesinde . (Braunschweig: Friedrich Vieweg & Sohn, 1872). Subsequently published in: ———, Gesammelte mathematische Werke, ed. Robert Fricke, Emmy Noether & Öystein Ore (Braunschweig: Friedrich Vieweg & Sohn, 1932), vol. 3, pp. 315–334.
25. ^ L. Kronecker, "Ueber den Zahlbegriff", [Crelle's] Journal für die reine und angewandte Mathematik, No. 101 (1887): 337–355.
26. ^ Leonhard Euler, "Conjectura circa naturam aeris, pro explicandis phaenomenis in atmosphaera observatis", Acta Academiae Scientiarum Imperialis Petropolitanae, 1779, 1 (1779): 162–187.
27. ^ Ramus, "Determinanternes Anvendelse til at bes temme Loven for de convergerende Bröker", in: Det Kongelige Danske Videnskabernes Selskabs naturvidenskabelige og mathematiske Afhandlinger (Kjoebenhavn: 1855), p. 106.
28. ^ Eduard Heine, "Einige Eigenschaften der Laméschen Funktionen", [Crelle's] Journal für die reine und angewandte Mathematik, No. 56 (Jan. 1859): 87–99 at 97.
29. ^ Siegmund Günther, Darstellung der Näherungswerthe von Kettenbrüchen in independenter Form (Erlangen: Eduard Besold, 1873); ———, "Kettenbruchdeterminanten", in: Lehrbuch der Determinanten-Theorie: Für Studirende (Erlangen: Eduard Besold, 1875), c. 6, pp. 156–186.
30. ^ Eric W. Weisstein, Sayı (MathWorld)
31. ^ . Merriam-Webster.com (İngilizce). Merriam-Webster. 13 Aralık 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 4 Ekim 2014. 
32. ^ Suppes, Patrick (1972). Axiomatic Set Theory (İngilizce). Courier Dover Publications. s. 1. ISBN . 
33. ^ Weisstein, Eric W. . Wolfram MathWorld (İngilizce). 5 Ağustos 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Temmuz 2020. 
34. ^ ^{a b} Berke Vardar, Açıklamalı Dilbilim Terimleri Sözlüğü. İstanbul: ABC Kitabevi. 2. baskı: 1988.

Kaynakça

• , Number, the language of science; a critical survey written for the cultured non-mathematician, New York, The Macmillan Company, 1930.^[]
• Erich Friedman, What's special about this number? 23 Şubat 2018 tarihinde Wayback Machine sitesinde .
• Steven Galovich, Introduction to Mathematical Structures, Harcourt Brace Javanovich, 1989, .
• , Naive Set Theory, Springer, 1974, .
• Morris Kline, Mathematical Thought from Ancient to Modern Times, Oxford University Press, 1990.
• Alfred North Whitehead and Bertrand Russell, Principia Mathematica to *56, Cambridge University Press, 1910.^[]
• Leo Cory, A Brief History of Numbers, Oxford University Press, 2015, .

Kaynak hatası: <ref> "lower-alpha" adında grup ana etiketi bulunuyor, ancak <references group="lower-alpha"/> etiketinin karşılığı bulunamadı (Bkz: )